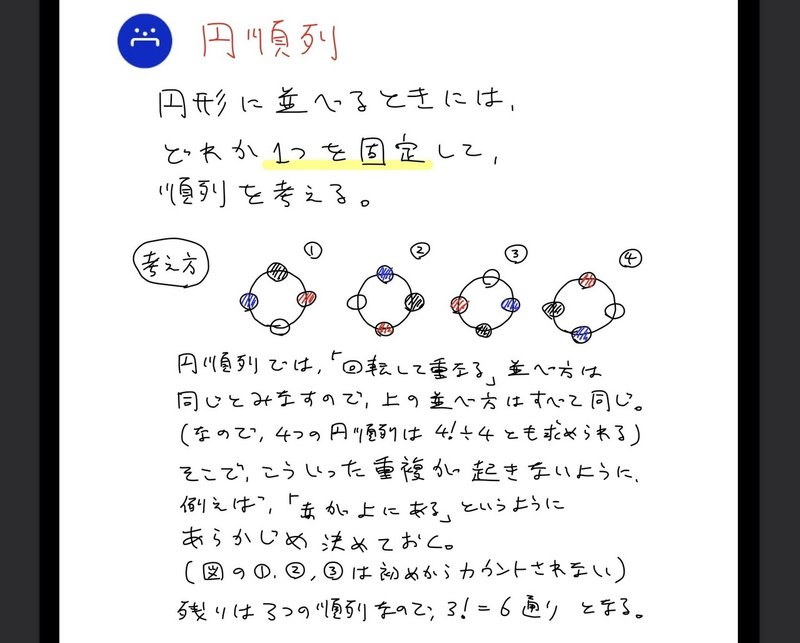
F 48通り 「QとRの2人を続けて並べる」という条件があるので、 まずQとRの2人を1つのグループにまとめ、 「1つのグループ」と「他の3人」の計4つの並び順 が何通りあるかを考える。 式) 4 P 4 = 4×3×2×1 = 24(通り) QとRの並び順については、「Q→R」と「RAmazoncojp 23最新版 史上最強SPI&テストセンター超実戦問題集 オフィス海 Japanese Books 次は順番を振らない円順列と、隣り合わせの順列の融合問題です。 基本的には両方の気をつけるべきポイントを抑えれば難なく解けます。 まず順番を振らない円順列の場合、 一人を固定すれば良い のでしたね。 先程同様にAを固定します。 次に
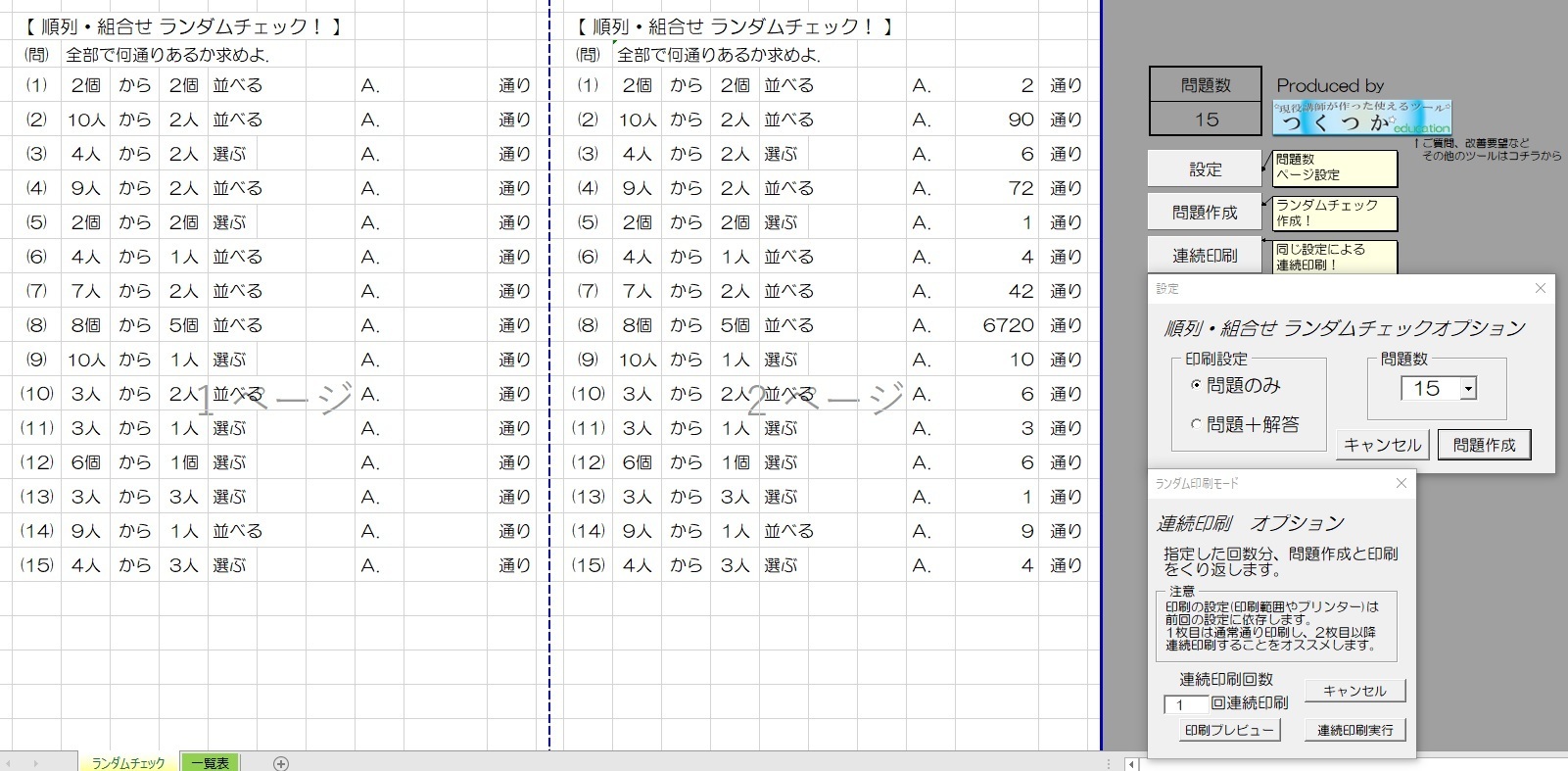
順列 組合せランダムチェック公開 現役講師が作った使えるサイト
順列 組み合わせ 問題集
順列 組み合わせ 問題集- 練習問題 順列と組合せの問題を混ぜました。 順列と組合せの違い 順列 :「選んで並べる」「ABとBA を区別してそれぞれ数える」 組合せ :「選ぶだけで並べない」「ABとBAは区別せず同じもの」 に注意しながら,考えてみてください。 例題3 (1) 5 場合の数や確率などは如何に問題を簡潔に考えられるかが重要になります。 突き詰めて考えると、 場合の数の解法は大きく分けて2パターン しかありません。 「和の法則」 と 「積の法則」 を如何に適切な形で使えるかが勝負の分かれ道といえます。 当




22年版 ダントツspiホントに出る問題集 ナツメ社
SUUGAKUJPは、大学入試の過去問を集めた数学に特化した学習サイトです。 全国の各大学における数学の入試問題を年度別に掲載し、利用シーンに合わせた無料学習が可能です。 続きはこちらから 超わかる! 高校数学 超わかる! 高校数学は、高校1年生ならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるのでまずは見分けがつかないと解くことができません。 組合せとは いくつかのものからいくつかのものを取り出して 並べる ことを 順列 と呼んでいました.ここでは,取り出したときの順序を考えない場合の数を考えてみましょう.そのような問題は 組合せ の問題と呼ばれています. 順列 → → 順序を考慮
Pb22 日本教育心理学会第 回総会発表論文集( 年) 小学生の概念的理解と手続き的知識の関係 ―順列と組み合わせを題材として― 大家まゆみ(東京女子大学) キーワード:概念的理解,手続き的知識,順列と組み合わせ 問題と目的順列・組合せ (章末問題) → 携帯版は別頁 順列,組合せ(章末問題) → 印刷用PDF版は別頁 解説 順列 異なる n 個のものから,異なる r 個のものを取ってできる順列の総数( ただし, 0 ≦ r ≦ n ) n P r = n!(n−r)!nnnnnn n個のもの全てを並べる順列は n P n =n (n1)・・・3・2・1 つまり1からnまでのすべての自然数の積である。 これを nの階乗 といい n!
高校数学A 場合の数 組分けは単純な問題は教科書レベルの基本問題であるが、実際には「モノが区別できるか否か」「組が区別できるか否か」「組の要素の個数が決まっているか否か」「要素の個数が0個の組があってもよいか」で求め方が変わる この記事では「順列」と「組み合わせ」の違いや見分け方について、公式や計算問題を通してできるだけわかりやすく解説していきます。 この \\(2\\) つはよく混同されるので、この記事を通してしっかりマスターしてくださいね!大人3人、子供4人がいる。ここから4人を選んでリレーチームを作りたい。 走る順番は何通りあるか? A 35通り B 4通り C 840通り D 1660通り E いずれでもない 大人2人、子供2人を選ぶとき、走る順番は何通りあるか? A 144通り B 2通り C 432通り D 840通り




2度解く 確率 順列と組合せ 大学入試過去問シリーズp O D 版 旺文社 本 通販 Amazon




ハヤト 勉強垢 Spi対策 0 59 07 不正解問題 5月8日 非言語 12 順列 組み合わせ 重複 円 応用 問題87 問題91 普通にキツすぎ 公務員試験の順列組み合わせはサクサク出来るのにspiの順列組み合わせは壊滅的 ハヤトの勉強報告 T Co
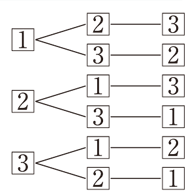
とあらわす。 例 4!=4・3・2・1 =24 6!=6・5・4・3・2・1 =7 n P r を階乗を用いて表す n P r =n (n1)・・・ (nr1) (nr)・・・2・1なぜ順列・組み合わせを学ぶのか プログラミング上の問題 に習った集合の演算を活用して,uを全体集合,aをuの部分集合としたときの, 𝑐(aの補集 合)を求めてください.組み合わせは、順序を持たない並べ方。例えば、{1,2}と{2,1}は同じもの。 例題(順列・組み合わせの基本) 1から3までの数が書かれたカードを2回引きます。そして、1回目と2回目に何を引いたか記録したい。 (1)引いたカードを戻さず、2回引く場合の順列の数を




数学a 重複組み合わせ問題 場合の数 チャート 実践例題集 自宅でできる受験対策ショップ ワカルー Wakaru



場合の数 順列と組み合わせの違いと並べ方問題の解き方
数に関する問題(1)約数・倍数 – No3 平面図形の移動 No8 正比例・反比例の関係 No9 数に関する問題(2)小数・分数 No11 立体思考に関する問題 No13 水深変化とグラフ No14 場合の数 -順列 組み合わせ・投票算-1 掲載経緯 東京女学館小学校の小野寺美賀先生は09年5月25日付けの朝日新聞の「花まる先生公開授業」 で紹介されました。それをきっかけとして、取材を行い、資料を提供してくださいました。本稿は提供して頂いた小野寺美香先生の資料のうち、場合の数の授業の意図を紹介します。なおワーク問題が分からなかった。3 / 数学公式集 / 順列 とても便利ですが、組み合わせと順列を勘違いしてらっしゃる方が両方のページにいらっしゃいます。




Spi3 円順列かどうかを判断する基準 注意点 順列 組み合わせ おいなりさんのspi完全攻略ロードマップ 就活 転職 Youtube




2度解く 確率 順列と組合せ 大学入試過去問シリーズp O D 版 旺文社 本 通販 Amazon
spi問題形式2:順列・組み合わせ ・順列・組み合わせ(並べ方と選び方) ある野球部の部員は、男子5人と女子3人の8人である。 (1)この8人の中から、部長と副部長を1人ずつ選びたい。選び方は何通りあるか。 a 14通り b 28通り c 56通り 場合の数を苦手とする受験生は多いです。 この分野は、目立った公式が順列の\\({}_n \\mathrm{ P }_k\\)と組み合わせの\\({}_n \\mathrm{ C }_k\\)くらいしかなく、解答方針を自力で立てないといけません。 場合の数に苦手意識を持つ人は、何でもかんでも数式と公式だけで解こうとしがち。パターンに ☆問題のみはこちら→順列と組み合わせの解法パターン(問題) ①約数に関する問題でまずすることは? →素因数分解 ②p⁰ →=1 ③条件が複数ある場合の数を考えるときはどのような条件から考えるか? →条件が厳しいものから順 "順列と組み合わせの解法パターン(問題と答え)"の続き




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生



同じものを含む順列の問題 京極一樹の数学塾
SPI 場合の数 問題31(順列)Study Pro(SPI) TOP SPI言語 SPI非言語 SPI英語 CAB 構造的把握力 TOP SPI非言語 場合の数小学6年生の算数 場合の数・順列 練習問題プリント ツイート 組み合わせ方、並べ方を、落ちや重なりがないように順序よく整理して、調べる方法を練習できる問題プリントです。 場合の数・順列(1) 答え 場合の数・順列(2) 答え 場合の数




北海道札幌厚別高等学校 数学応用 学校設定科目 順列 組合せの違いを理解する 竹之内 康秀教諭




Spi 非言語問題 順列 組み合わせの応用 就活の答え




高校数学a 重複組合せ Nhr 受験の月




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




高校数学a 組分け問題全パターン 受験の月



大学入学共通テスト準備問題集 数学i A チャート式の数研出版



1




場合の数 順列 組合せ のブログ記事一覧 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




高校数学a 組合せの基本と順列との関係 Ncrの性質 受験の月



順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典
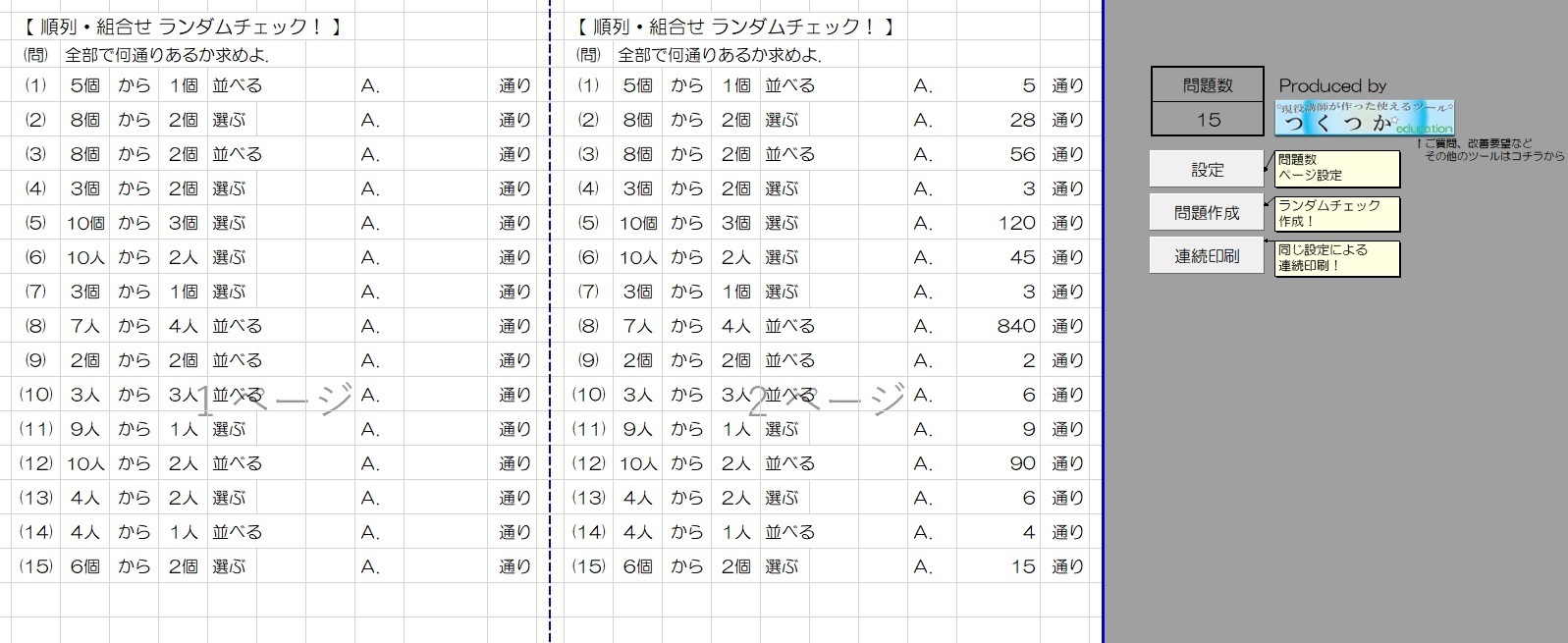



順列 組合せランダムチェック公開 現役講師が作った使えるサイト




円順列の応用問題5選 難問2選を解説 順列との違いとは 遊ぶ数学




高校数学a 一定の順序を含む順列 受験の月




順列と組み合わせの公式とその違い 問題付き 理系ラボ




組合せは1時間で解けるようになる 外資系コンサルタントが主夫になったら




基礎力完成 確率 順列と組合せ 大学入試過去問シリーズp O D 版 旺文社 本 通販 Amazon



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ
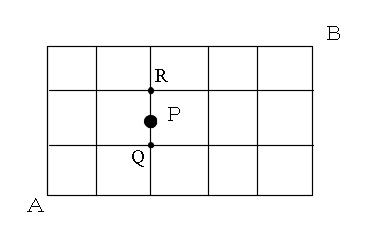



組み合わせの考え方と公式 組み分けと道順を求める問題の解き方




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




22年版 ダントツspiホントに出る問題集 ナツメ社




基礎力完成 確率 順列と組合せ 大学入試過去問シリーズp O D 版 旺文社 本 通販 Amazon



順列と組み合わせ 算数用語集




順列組合せ 確率のプリント集




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




ハヤト 勉強垢 Spi対策 0 59 07 不正解問題 5月8日 非言語 12 順列 組み合わせ 重複 円 応用 問題87 問題91 普通にキツすぎ 公務員試験の順列組み合わせはサクサク出来るのにspiの順列組み合わせは壊滅的 ハヤトの勉強報告 T Co




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




3講 順列 1章 場合の数と確率 問題集 高校数学a



2




高校数学無料問題集 数a 第1章 場合の数と確率 順列 桝 ます Note




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




重複順列の問題6選とは 公式よりも応用問題の解き方が大切です 遊ぶ数学




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ



高校数学無料問題集 数a 第1章 場合の数と確率 順列 桝 ます Note




5分でわかる Spi 非言語 の順列 組み合わせの答え方 Webテスト対策講座 Youtube



順列 組合せの問題がわからなく 教えてくださいm Mある委員会のメンバ Yahoo 知恵袋




3講 順列 1章 場合の数と確率 問題集 高校数学a




Spi 数学 対策問題 組み合わせ 順列 しかくのいろは




なぜ 同じものを含む順列の公式と使い方について問題解説 数スタ




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



1




順列と組み合わせの公式とその違い 問題付き 理系ラボ




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典




3講 順列 1章 場合の数と確率 問題集 高校数学a



2




高校数学無料問題集 数a 第1章 場合の数と確率 順列 桝 ます Note




数学 a基礎問題精講 五訂版 旺文社



確率問題全般 京極一樹の数学塾




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学




高校数学無料問題集 数a 第1章 場合の数と確率 順列 桝 ます Note



Spi M54e217p7lcis9d Com Jyunretu Kumiawase Q1



9 3 確率の計算 順列 組み合わせ 統計学の時間 統計web



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




場合の数 順列 組合せ のブログ記事一覧 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




順列 組合せランダムチェック公開 現役講師が作った使えるサイト




順列と組み合わせの公式とその違い 問題付き 理系ラボ




順列と組み合わせの公式とその違い 問題付き 理系ラボ




過去問演習 解説 場合の数 順列 組合せ 数学 基礎 コメディカル受験対策講座



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




3分で分かる 順列と組み合わせの違いと公式をわかりやすく 練習問題つき 合格サプリ



順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典



順列と組み合わせの違い カンタンな見分け方を教えます Studyplus スタディプラス



spi対策問題集 教材 問題集 関口心理テストセンター




重複組合せ 組合せ 重複順列に関する問題 2018年度前期日程高知工科大学の入試問題 身勝手な主張




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




順列と組み合わせの公式とその違い 問題付き 理系ラボ



1



Q Tbn And9gctdg7qzyj8jefiumjmojygwqcr6bhmbi685zwhir13rni5bkqx6 Usqp Cau




3講 順列 1章 場合の数と確率 問題集 高校数学a



同じものを含む順列の問題 京極一樹の数学塾



2




高1 数a 場合の数 4 組合せ 高校生 数学のノート Clear



数a順列組み合わせ 2番と3番の問題について なぜ分数になる Yahoo 知恵袋




高校数学無料問題集 数a 第1章 場合の数と確率 順列 桝 ます Note




重複を許す組み合わせ Hを使った公式 仕切りを使った考え方を解説 数スタ



spi頻出問題7 順列 組み合わせ



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




組合せ論パーフェクト マスター 日本評論社




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生




順列と組み合わせの公式とその違い 問題付き 理系ラボ
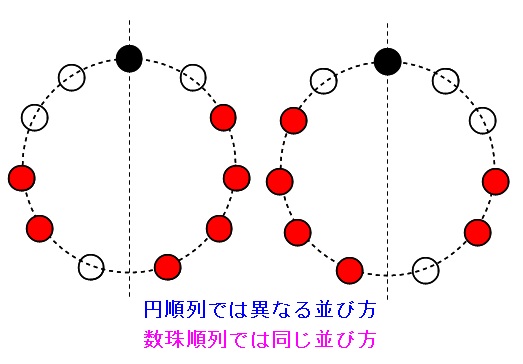



円順列と数珠順列の考え方や公式と問題の解き方




順列と組合せの違いと例題 高校数学の美しい物語




重複組合せ 組合せ 重複順列に関する問題 2018年度前期日程高知工科大学の入試問題 身勝手な主張




中学数学 場合の数




順列と組み合わせ 算数用語集




場合の数 順列 組合せ 2020年度前期日程の神戸大学文系の入試より 身勝手な主張




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学




23年度版7日でできる spi 頻出 問題集 高橋書店




過去問演習 解説 場合の数 順列 組合せ 数学 基礎 コメディカル受験対策講座




21最新版 史上最強spi テストセンター超実践問題集 オフィス海 本 通販 Amazon




高校数a 組合せ 同じものを含む順列 オンライン無料塾 ターンナップ Youtube



0 件のコメント:
コメントを投稿