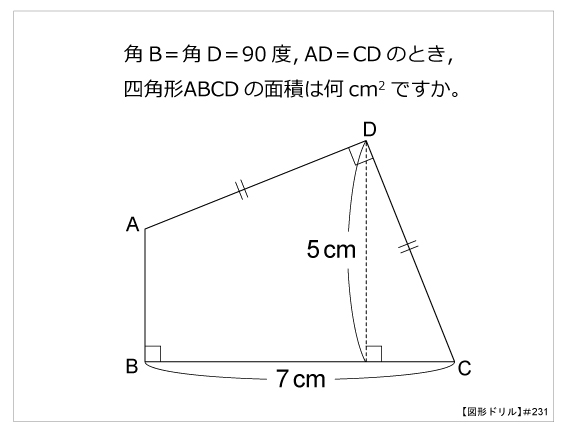
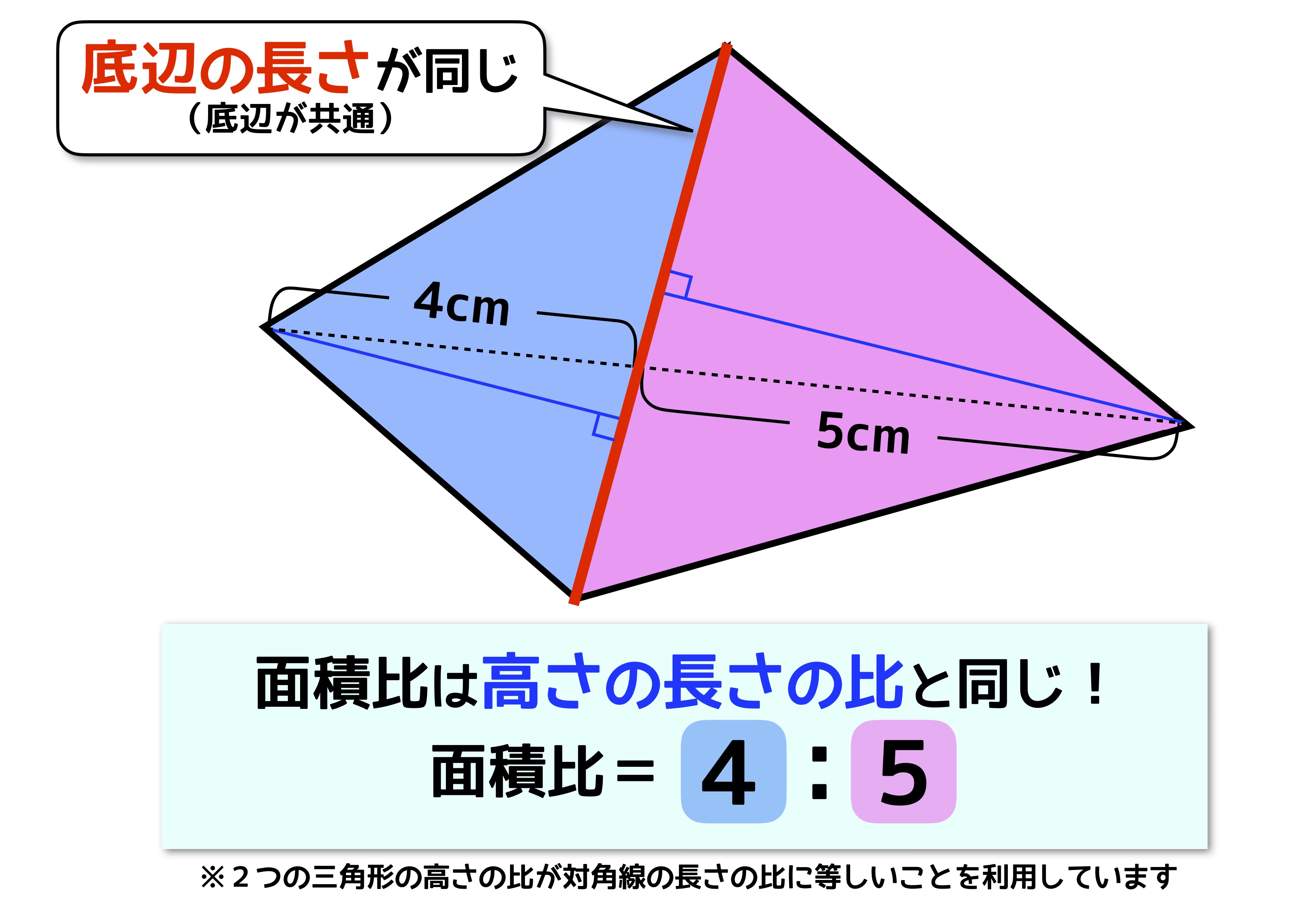
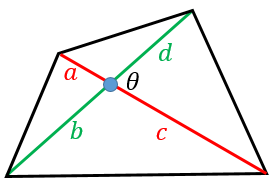
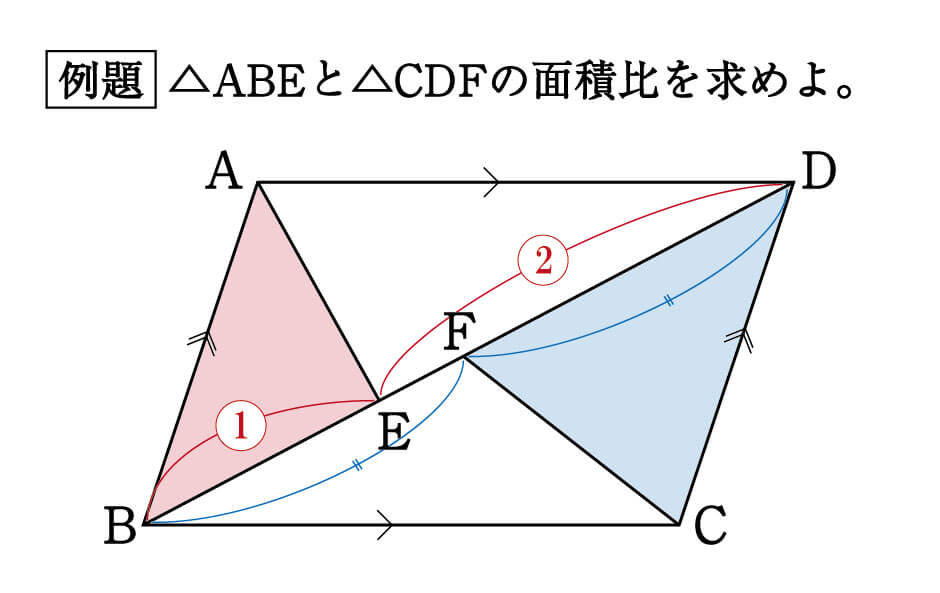
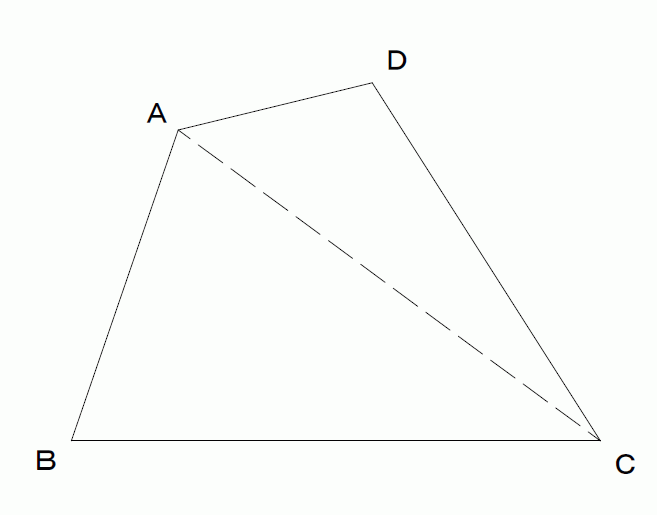
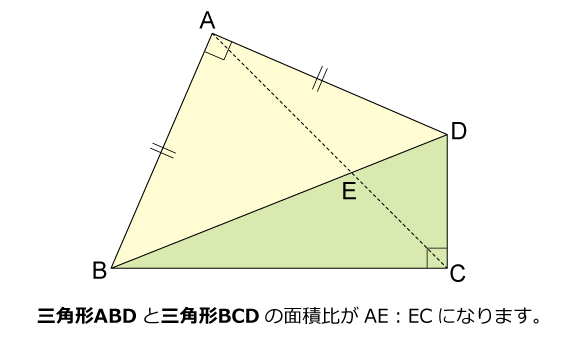
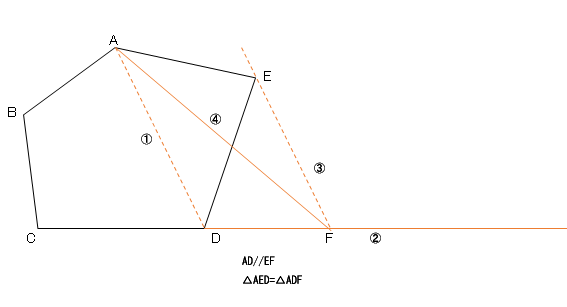
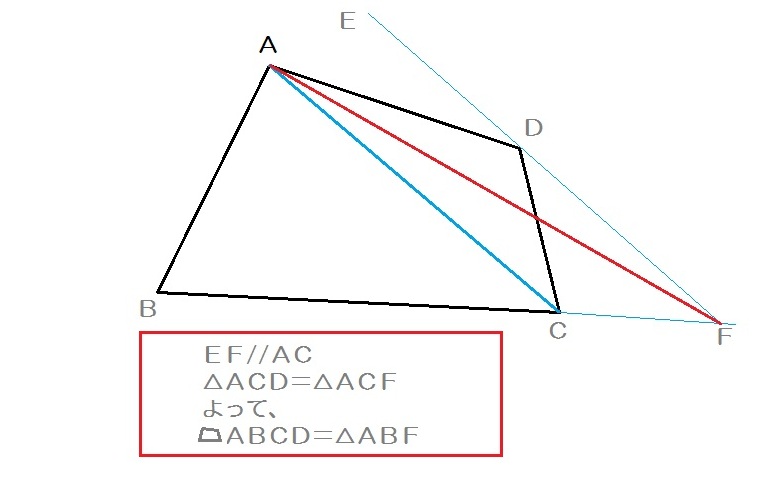
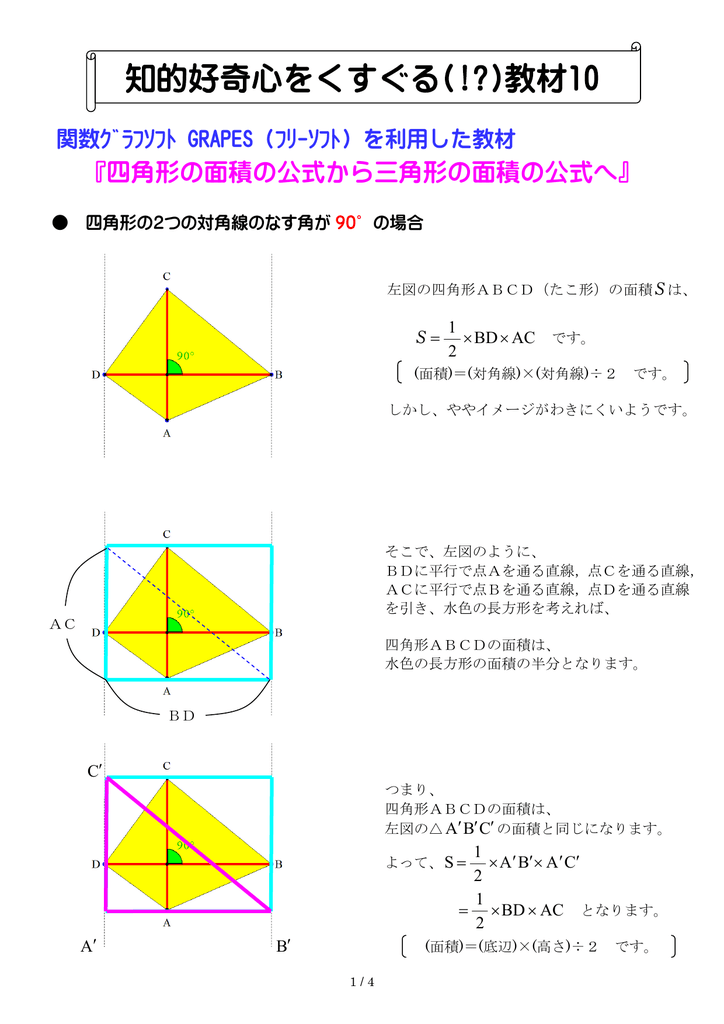
平行線と面積の性質から acd= aceとなります。 よって $${四角形abcd= abc+ acd}$$ $${= abc+ ace}$$ $${= abe}$$ となるので abeは四角形abcdと面積が等しい三角形だということがわかります。
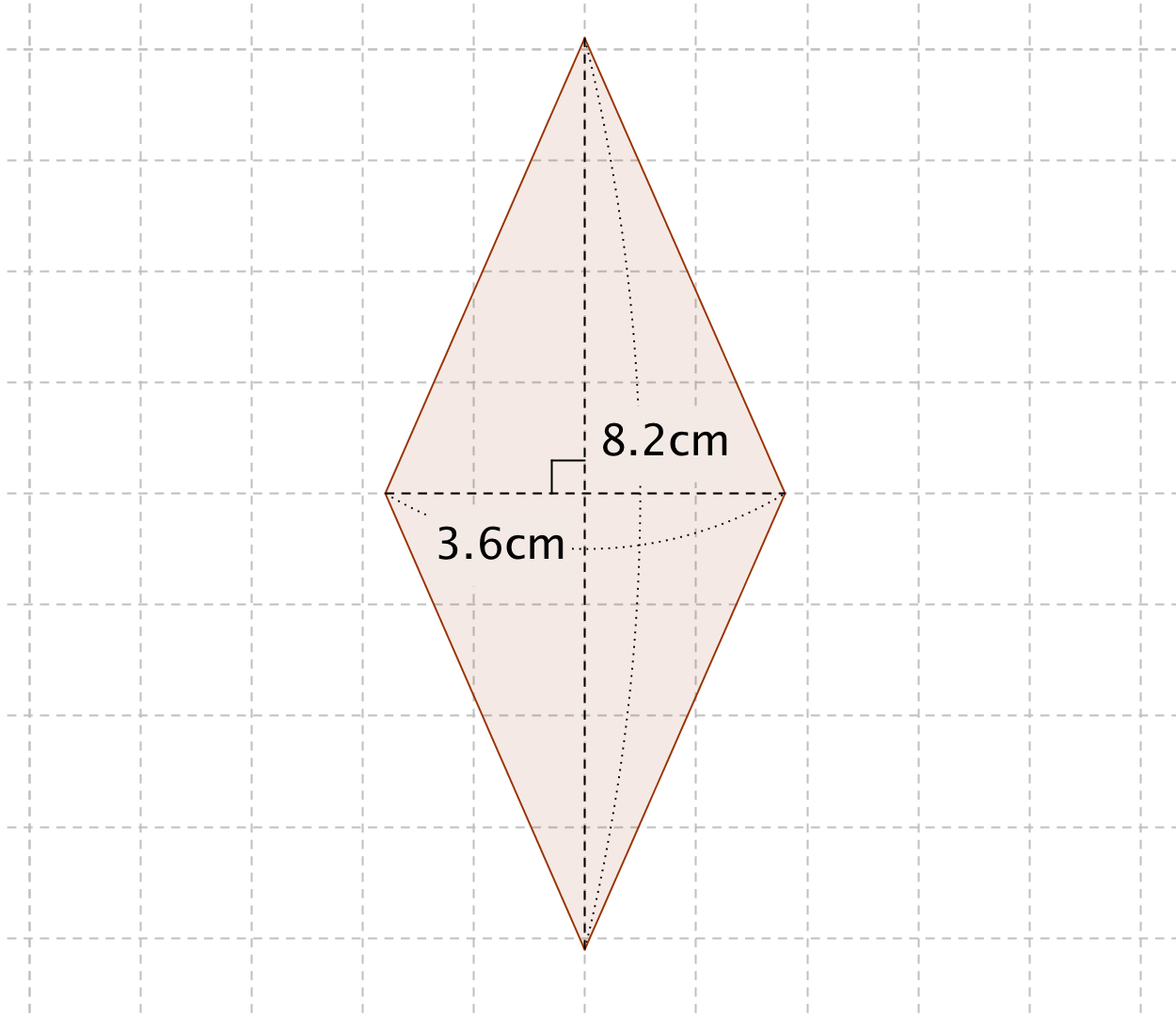
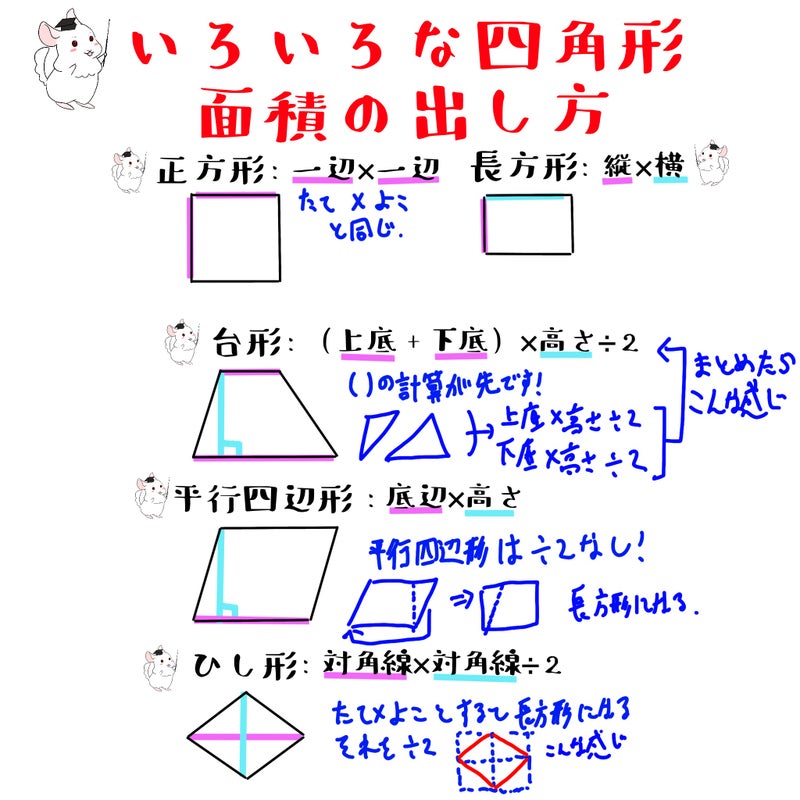
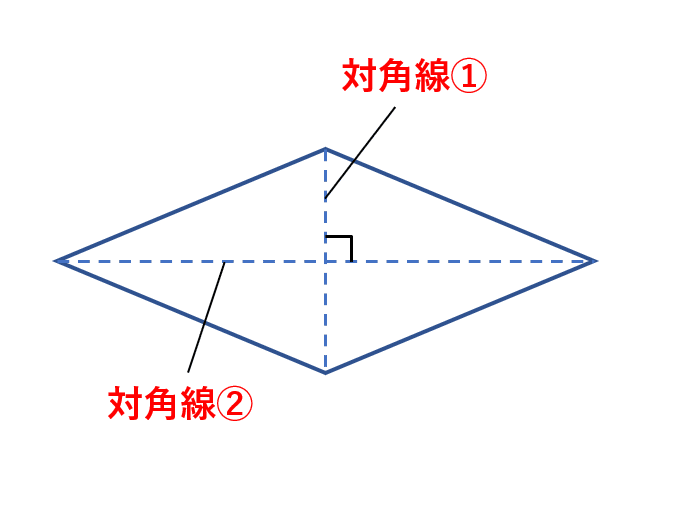
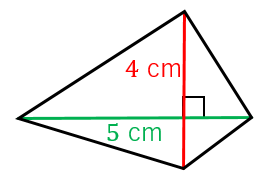
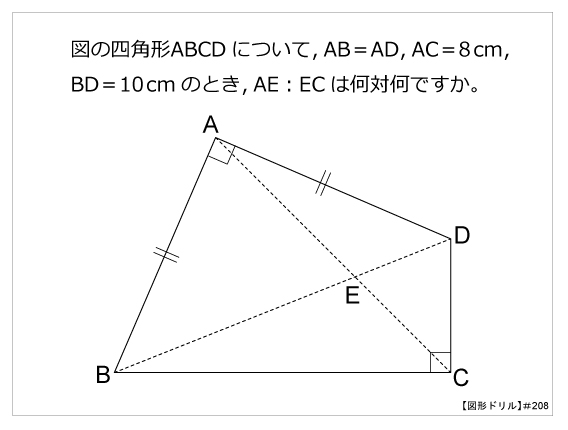
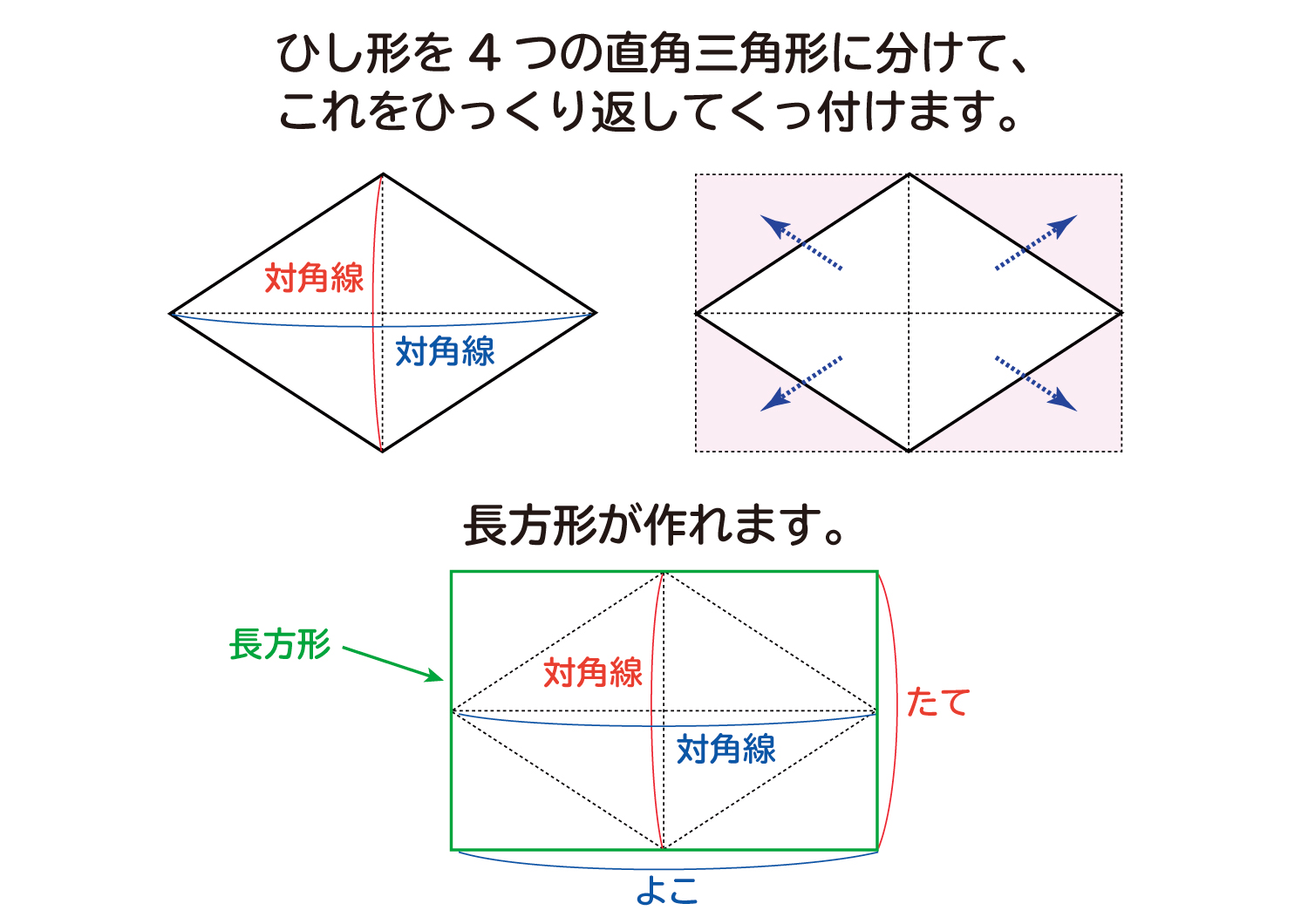
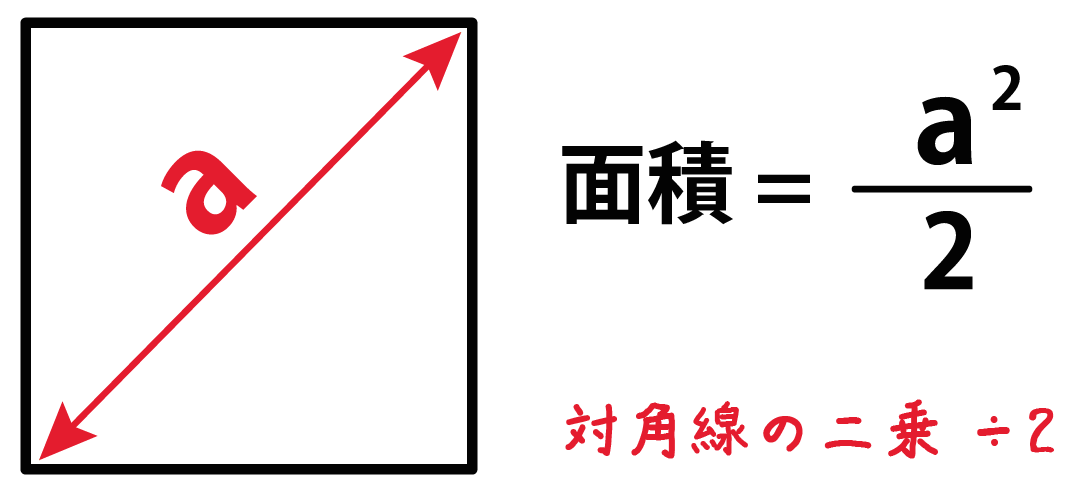
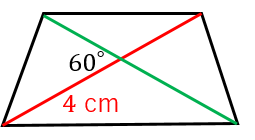
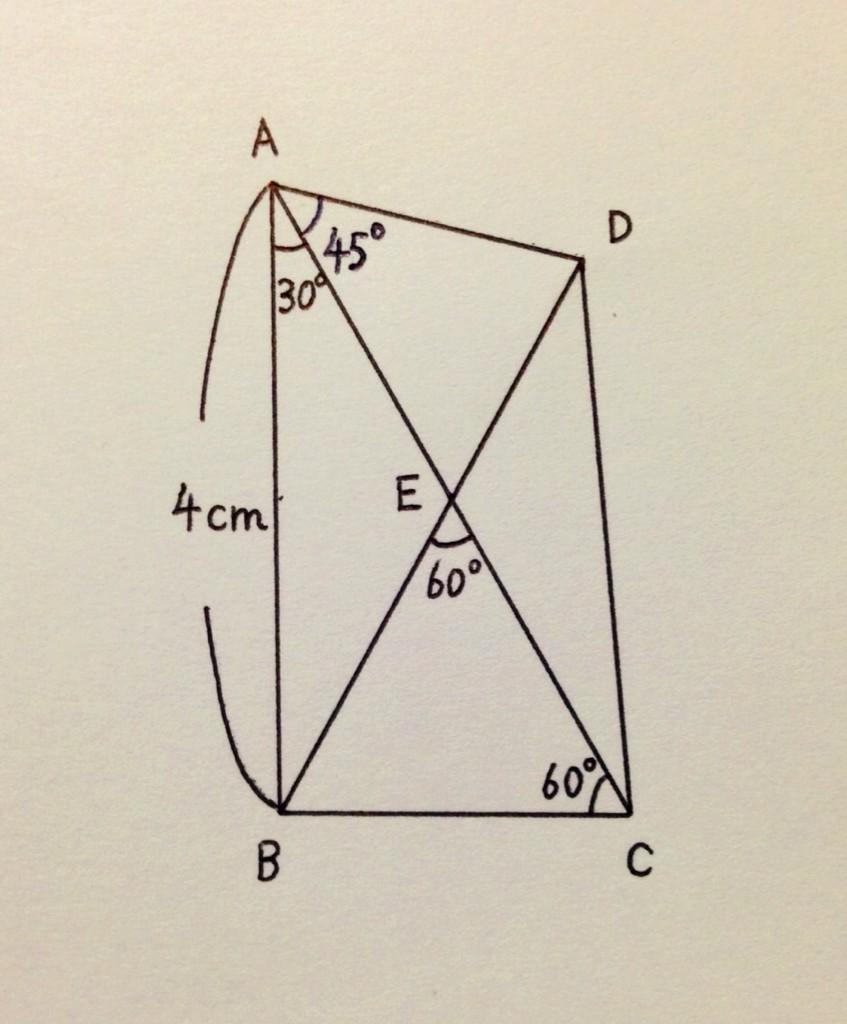
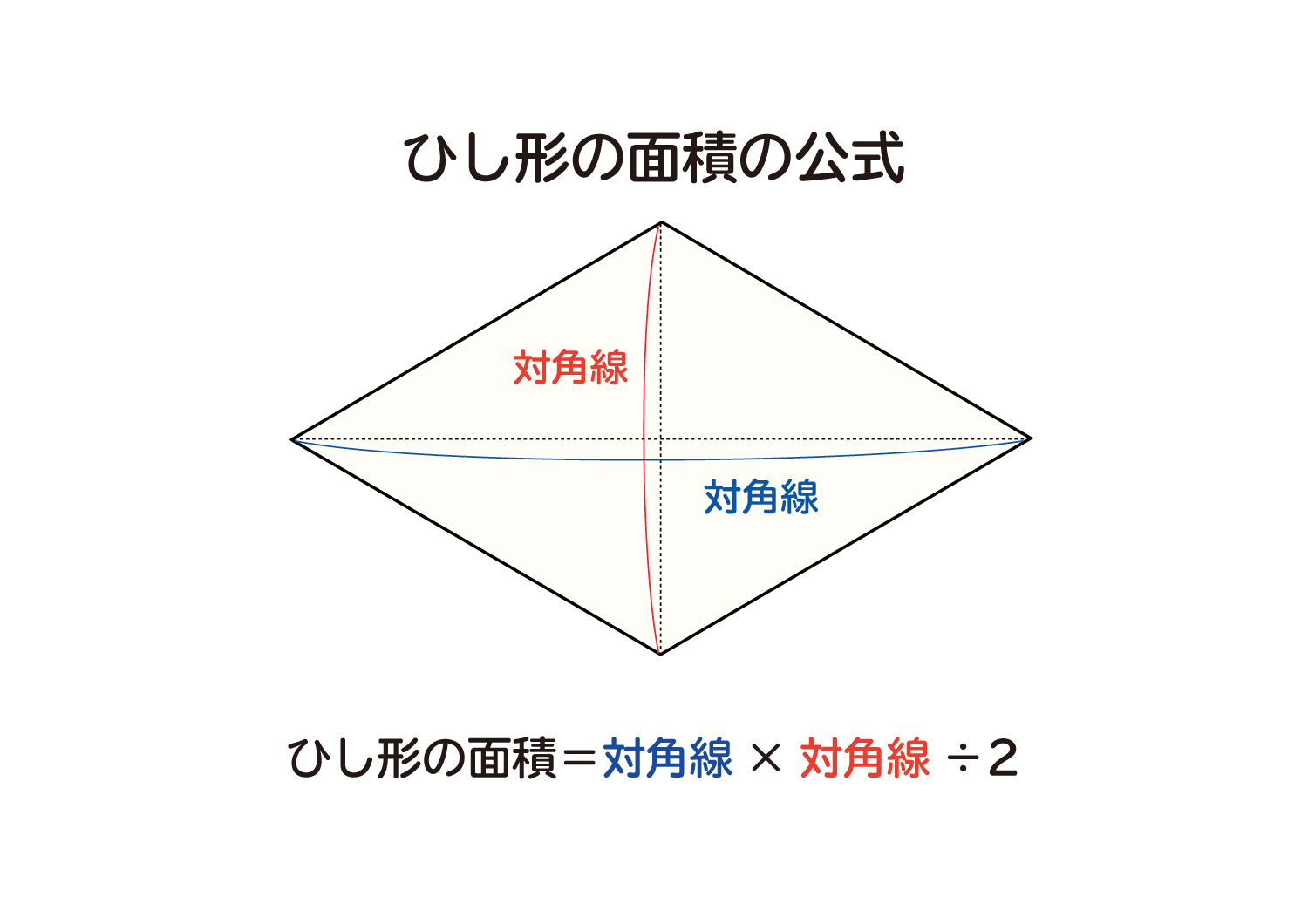
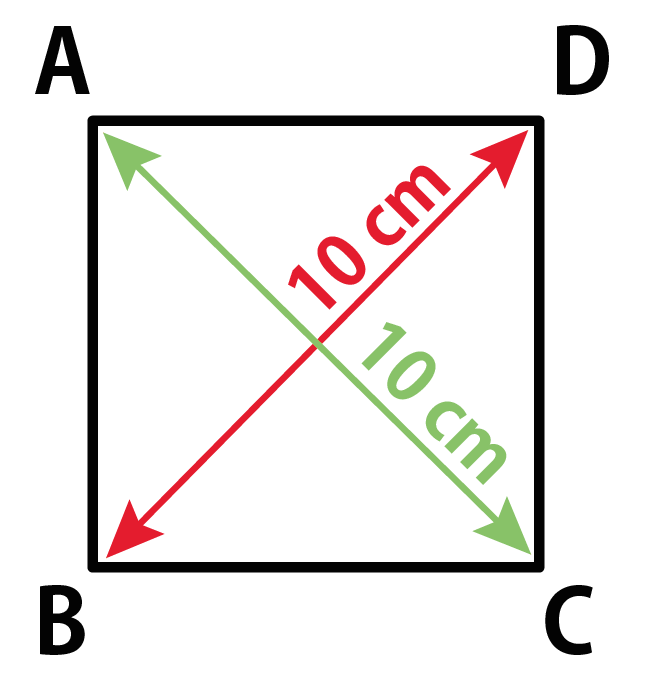
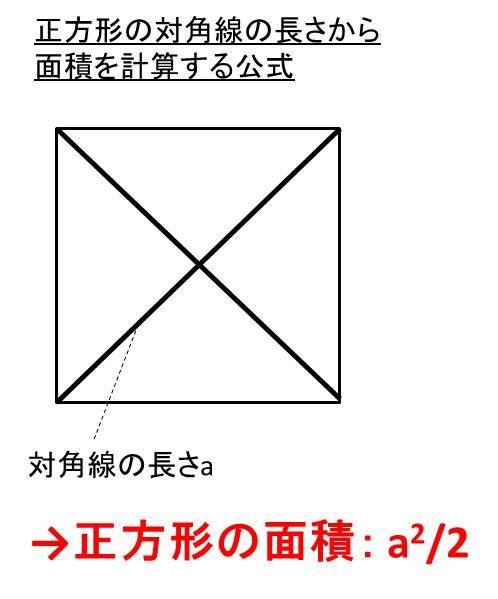
四角形 対角線 面積-ひし形の面積の求め方は 縦の対角線×横の対角線÷2 です。 下図をみてください。 これがひし形です。 ひし形とは全ての辺の長さが等しい四角形です。 またひし形の2つの対角線は必ず直交します。 上図の縦方向の対角線a、横方向の対角線bを掛けて2 四角形の4つの辺の長さ \(a,b,c,d\) に加え、どちらか一方の対角線の長さ \(e\) が分かっている場合。 四角形を2つの三角形に分けてから各三角形の面積 \(S_1,S_2\) をヘロンの公式を使って求め、それらを合計することで四角形の面積を求めることができます。
四角形 対角線 面積のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
 |  | |
「四角形 対角線 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「四角形 対角線 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
 |  |  |
「四角形 対角線 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 | ||
「四角形 対角線 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | 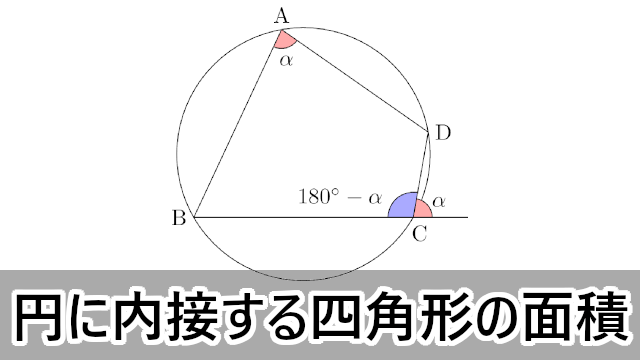 |
 |  | |
「四角形 対角線 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 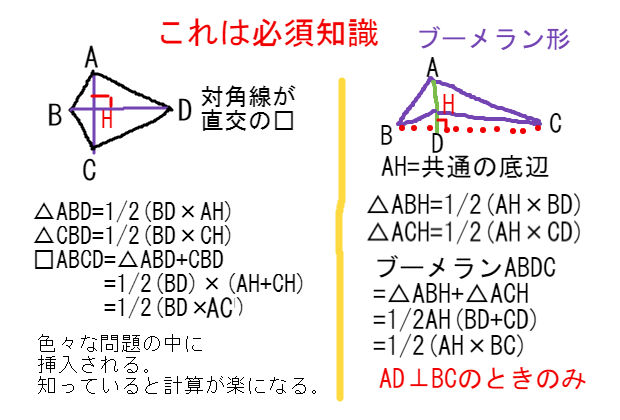 | |
 |  |  |
 | 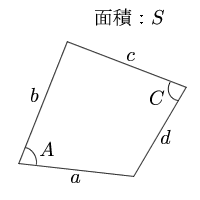 |  |
「四角形 対角線 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
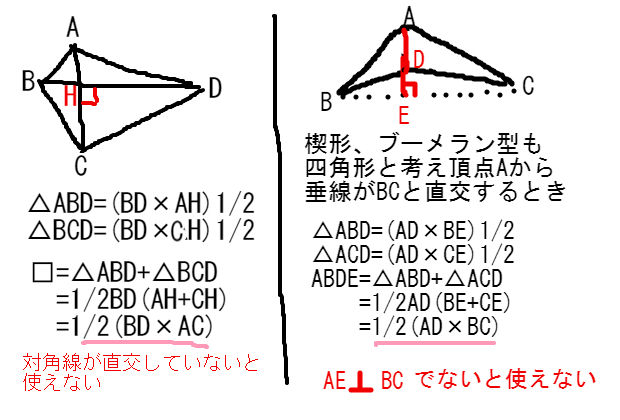 |  | |
 |  |  |
 |  | |
 | 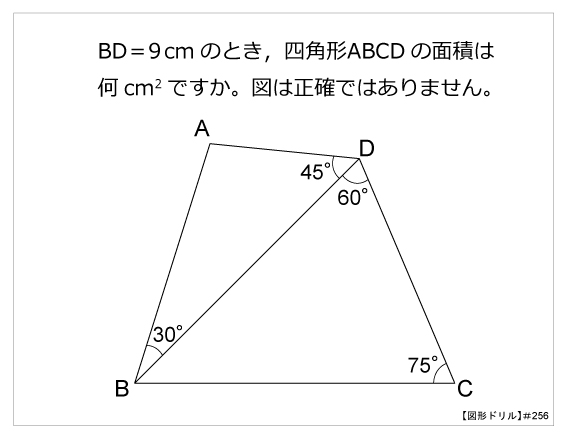 |  |
「四角形 対角線 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
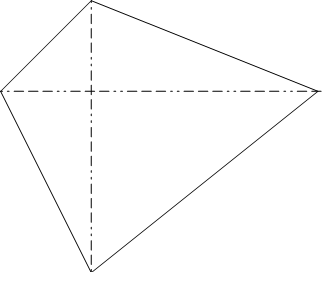 |  |  |
 | 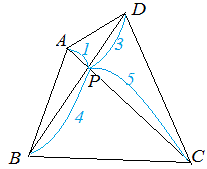 |  |
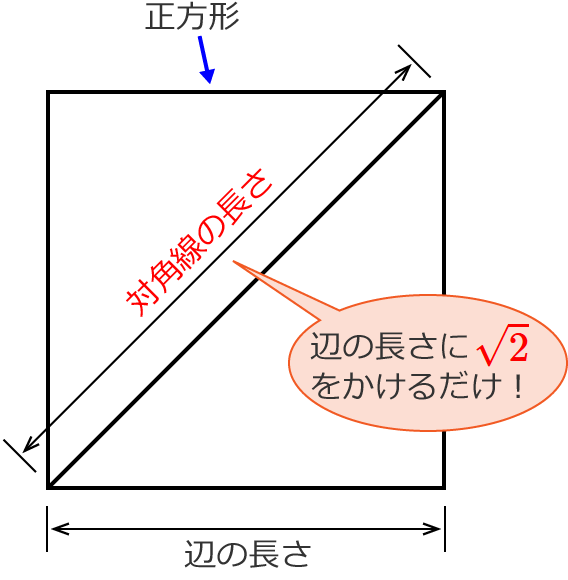 |  | |
「四角形 対角線 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
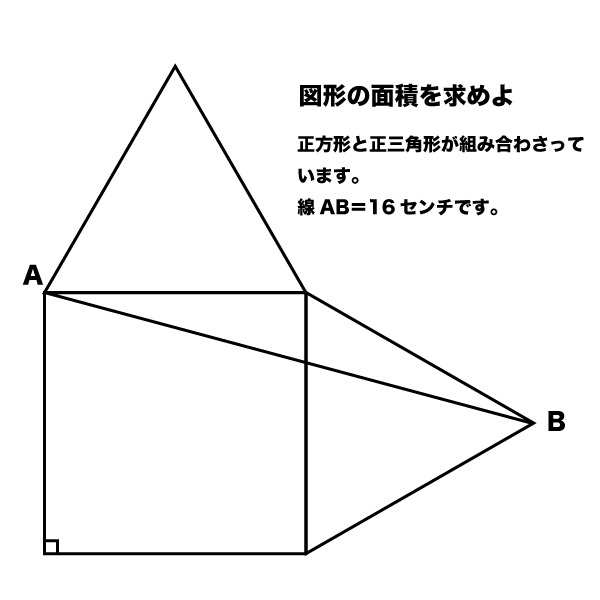 | 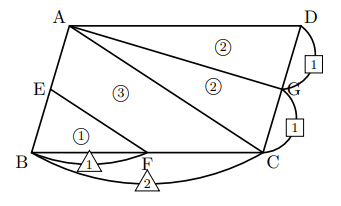 | 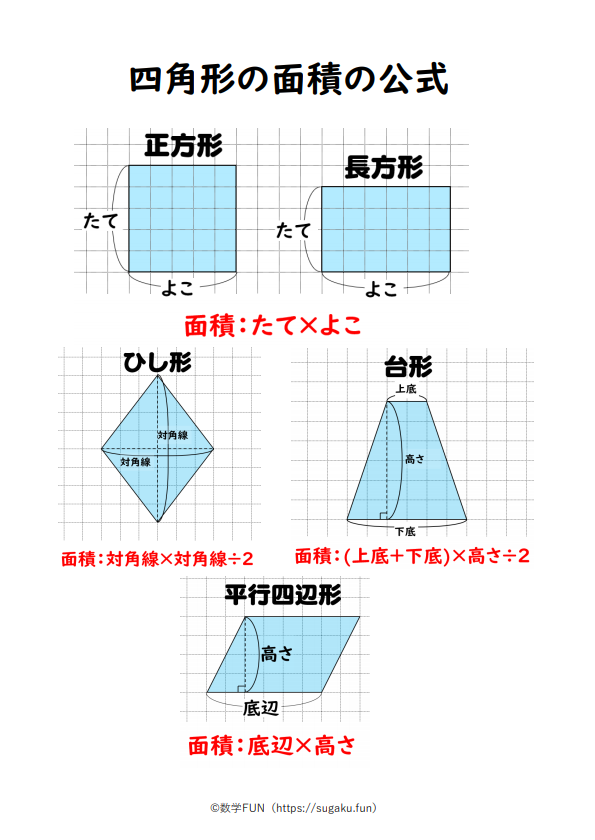 |
 | 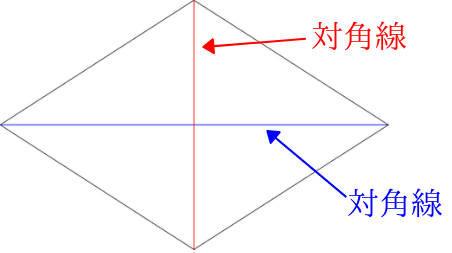 |
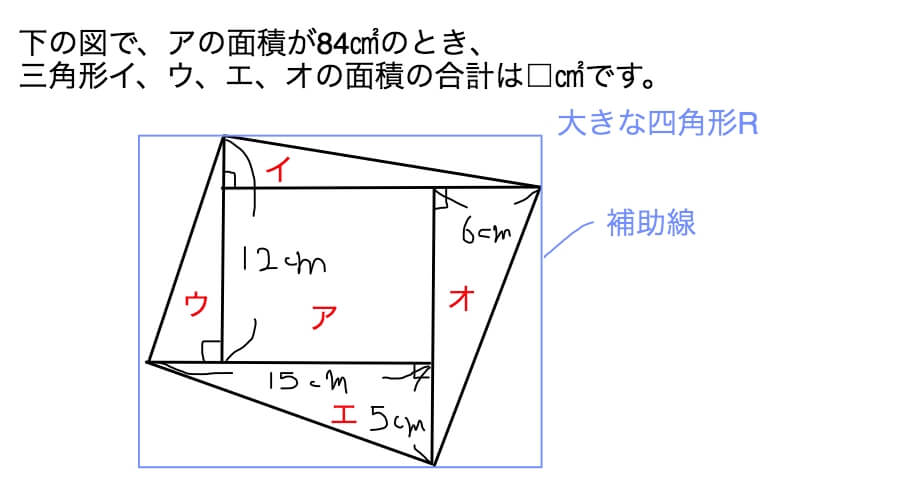
小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題四角形を対角線によって三角形に分割して面積を求める方法を知り、三角形で分 割する方法を使うとどんな四角形や多角形も面積を求めることができることを理解 する。 本時の目標 四角形を三角形に分割する考え方を用いて四、。角形の面積を求めること





0 件のコメント:
コメントを投稿